A look at a paper that explores possible assumption failures of CAPM that would explain the low volatility anomaly.
Previously
We’ve talked about CAPM before, in particular:
There has also been substantial talk about low volatility investing.
The paper
The paper is “Explanations for the Volatility Effect: An Overview Based on the CAPM Assumptions” by David Blitz, Eric Falkenstein and Pim Van Vliet.
A quote:
One of our findings is that not just one or two, but at least four out of the five CAPM assumptions are involved with the various explanations. Second, our overview may help to develop tests for discriminating between different explanations. Third, a key takeaway of our analysis is that, contrary to the popular notion that anomalies in financial markets are driven by irrational investor behavior, various explanations for the volatility effect are actually rooted in rational investor behavior, especially when considered in the context of institutional constraints.
The five assumptions of the CAPM are (in their words):
- there are no constraints, e.g. on leverage and short-selling
- investors are risk-averse, maximize the expected utility of absolute wealth and care only about the mean and variance of return
- there is only one period
- information is complete and rationally processed
- markets are perfect, i.e. all assets are perfectly divisible and perfectly liquid, there are no transaction costs, there are no taxes and all investors are price takers
The key conflict between the low volatility anomaly and CAPM is that the positive linear relation between beta and expected return posited by CAPM tends not to hold empirically. The post “Beta and expected returns” shows a few cases. Figure 3 of that post — presented here as Figure 1 — is an example.
Figure 1: Returns versus beta estimate at start 2009. 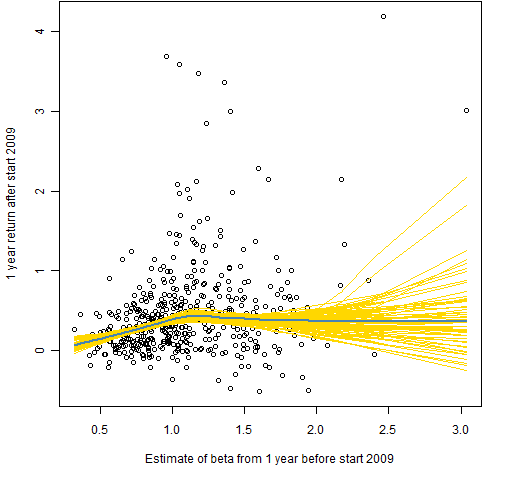 This picture is not especially atypical, and it makes clear that the low volatility anomaly would be better called the high volatility anomaly.
This picture is not especially atypical, and it makes clear that the low volatility anomaly would be better called the high volatility anomaly.
Another quote:
It is important to note which explanations are profoundly irrational, such as the winner’s curse, because these are presumably more ephemeral, like a trading rule that exists until people see the profit opportunities it generates. If, on the other hand, the irrationality comes from constraints or agency issues that drive managers towards higher volatility stocks, the effect is not likely to disappear unless some major industry-wide changes would be implemented.
Models
The “M” in CAPM stands for Model. That’s correct. CAPM is a fine model. The problem is that there has been a concerted and sustained effort to turn it into CAPT as in Truth — a prime example of Models Behaving Badly. The paper is an example of using the model in quite a good way.
All models are wrong, some models are useful.
— George Box (1919 Oct 18 — 2013 Mar 28)
Photo via Wikipedia.
Summary
The paper should be interesting for how it dissects the problem even if you don’t care about low volatility.
Epilogue
Our ideas held no water
But we used them like a dam
Oh, and we carried it all so well
from “Missed the Boat” by Isaac Brock

Pingback: Monday links: amazingly unpredictable | Abnormal Returns
Pingback: The low vol effect and time frame mismatches | Abnormal Returns