A herd of heuristic algorithms is compared using a portfolio optimization.

Previously

“A comparison of some heuristic optimization methods” used two simple and tiny portfolio optimization problems to compare a number of optimization functions in the R language.

This post expands upon that by using a portfolio optimization problem that is of a realistic size (but still with an unrealistic lack of constraints).

Test case

The optimization problem is to select 30 assets out of a universe of 474 and find their best weights.  The weights must be non-negative and sum to 1.  The integer constraint is binding — more than 30 assets in the portfolio can give a better utility.  The utility is mean-variance.

Each optimizer was run 100 times.  To have a fair comparison the amount of time that each run took was controlled to be about 1 kilosecond.  (There are a couple that also have runs that take much less time.)

The timings are not all particularly close to 1000 seconds, but they are probably all close enough that the picture is minimally distorted.

Besides, the timing (on Windows) seems dodgy.  It is supposed to be timing only the compute time (not elapsed time), but the timings don’t seem to be following a constant plus noise model.  Figure 1 shows an example of the timing.

Figure 1: The compute time reported for genopt in the order of the runs. 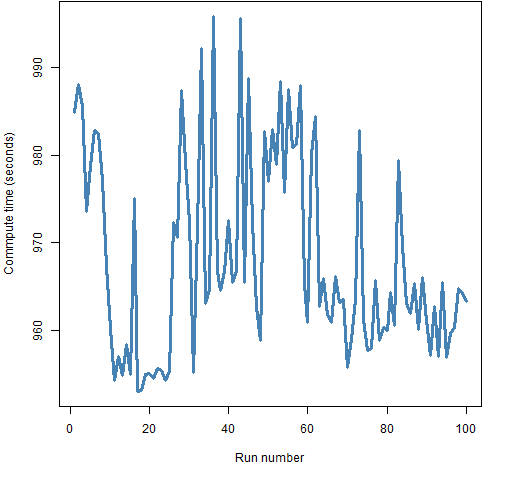The timings are a bit suspect, but should be good enough.

The optimizers

Most of the optimizers used in “A comparison of some heuristic optimization methods” are also used here.  The exception is the functions from NMOF because they don’t have explicit box constraints (there is a mechanism for imposing constraints though).  The only unconstrained method that was run was the SANN method of the optim function.

Three methods were added.

pso package

The psoptim function from pso implements a particle swarm algorithm.

nloptr package

The Controlled Random Search (CRS) method was done via the nloptr function in the nloptr package.

This has the unexpected behavior of not respecting default values of arguments in the function to be optimized.  You need to specify additional arguments to the function even when they have default values.

cmaes package

The Covariance Matrix Adapting Evolutionary Strategy is implemented in the cmaes package.

When the version from CRAN (1.0-11) was used on this problem, it got nowhere.  The results presented here are from an R-forge version.  Apparently the difference is the default values for control variables.  Adjusting default values is a work in progress.

Results

Portfolio Probe consistently gets the same (best) answer in about 3 to 4 seconds.

Figure 2 shows the distribution of deficiencies from the best answer for the methods.

Figure 2: Difference in utility from optimal (ordered by median). 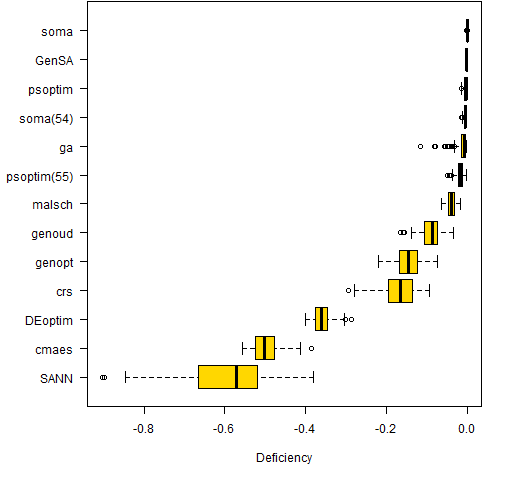The methods “soma(54)” and “psoptim(55)” are sets of runs where the time was significantly less than 1000 seconds.  The number in parentheses is the mean time in seconds for the runs.

Figure 3 has the same information as Figure 2, but the sign of the numbers is changed and the plot is on the logarithmic scale.

Figure 3: Logarithm of negative difference in utility from optimal (ordered by median).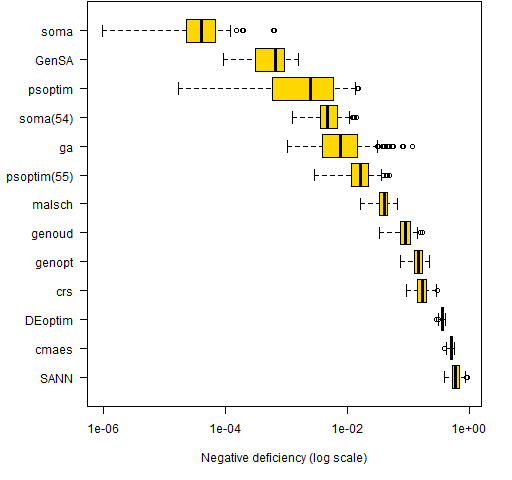

Comments

Private correspondence with Enrico Schumann improved this section.

Defaults

This is not a comparison of algorithms.  This is a comparison of algorithms with their mildly modified default values on one problem.

The importance of default parameters is evident with cmaes.  The CRAN set didn’t even get out of the starting gate.  The set that was used didn’t compare very favorably with the other optimizers.  But it seems certain that there is a set of control parameters for it that would do very well.

Applications matter

The problem that is being solved has an effect on which algorithms (plus control parameters) work best.  There is not a uniformly best algorithm.

Experimentation is useful

Experimenting with different algorithms and their settings is likely to pay off if you are doing the same sort of optimization repeatedly.

What is good enough?

There is almost always a point at which moving to a more optimal answer is not of practical relevance.  That point will of course depend on the actual problem.

“What is good enough for portfolio optimization?” is an excellent question that I don’t think anyone has a good answer to.  It does obviously depend on the quality of the inputs — if the inputs are complete garbage, then it doesn’t matter how close to optimal you are.  (The correct answer in that case is not to trade at all.)

Clustering

Both soma and psoptim (and perhaps others) get relatively good answers within a minute, but then they never seal the deal, so to speak.  They don’t get especially close to the best objective.

You may naively think that the longer runs would be scattered between where they are after a minute and the best solution.

Given:

• a problem
• an algorithm
• its control parameters
• the amount of time it runs

then there is an expected value for that random process.  The Law of Large Numbers says that the actual result for any run is likely to be close to the expected value. That is the clustering we are seeing.

One star

There is one algorithm (besides Portfolio Probe) that has done well in all of the problems in this and the previous comparison: GenSA.

We don’t know how specific that is to the problems posed and its default parameters.  But it seems worth keeping an eye on it.

Appendix R

The functions and data to reproduce this analysis are in heuristic_objs2.R (4 MB). The utility that Portfolio Probe achieves is -0.35776787228876. The non-zero optimal weights (to six decimal places) are in optimalWeightsAll.csv.

In case you want to test routines on these problems outside R: the variance is in varianceall.csv (4 MB) and the expected return vector is in expectedreturnsall.csv.