Why returns have a stable distribution
As “A tale of two returns” points out, the log return of a long period of time is the sum of the log returns of the shorter periods within the long period.
The log return over a year is the sum of the daily log returns in the year. The log return over an hour is the sum of the minute log returns within the hour.
Returns have some distribution. The set of distributions where their sums still have the same distribution are called stable distributions. So log returns have a stable distribution.
Why returns have a normal distribution
There is a special distribution within the class of stable distributions called the normal distribution. It is the only one that has a finite variance.
The Central Limit Theorem tells us conditions when the distribution of a sum is normal (to a good approximation). Actually there is more than one Central Limit Theorem. Figure 1 shows the single theorem idea, while Figure 2 shows the actual case.
Figure 1: Sketch of The Central Limit Theorem. 
Figure 2: Sketch of The Central Limit Theorems. 
The commonality of the assumptions in Figure 2 can be summarized as:
- No giants among the peons
- Not too much dependence between the peons
Returns obey these criteria. Therefore log returns have a normal distribution.
That applies to individual assets. The returns of an index — which is the weighted average of a number of assets — has even more reason to be normal. Even if the returns of the individual assets were not normal, the averaging over assets would mean that the index returns would be normal.
Data
The previous two sections are exquisitely reasoned. So imagine my disappointment when people try to say that returns are not normally distributed.
Figure 3 shows the daily log returns of the S&P 500 over about six decades in the form of a normal QQplot. Based on the variability of the middle half of the data, the most extreme returns we should have seen during that period was about 3%. We’re not far off.
Figure 3: Normal QQplot of 6 decades of daily S&P 500 log returns.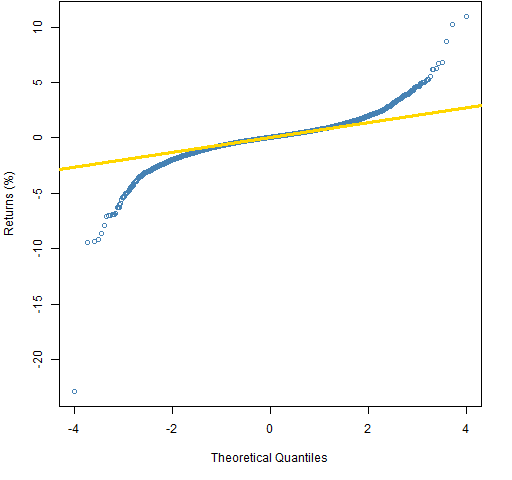 
A reason that the distribution would not be exactly normal is because of volatility clustering — that some periods have higher volatility than others. We can look at the residuals from a garch model to remove that effect. This is done in Figure 4.
Figure 4: Normal QQplot of 6 decades of daily GARCH residuals from S&P 500 log returns.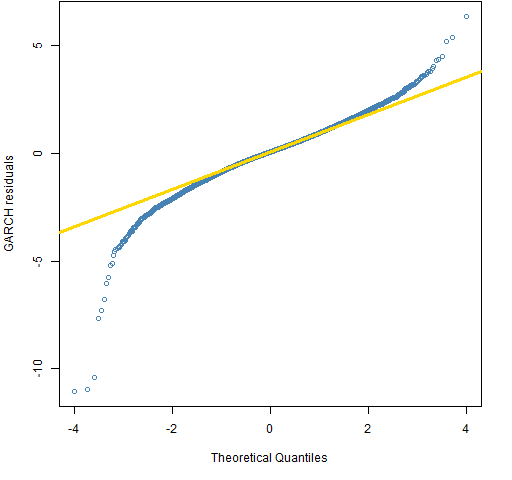 
Now that’s better, isn’t it? If you think that volatility clustering negates the logic that leads us to the stable distribution conclusion, then, well, uh … think something else.
We don’t have to rely on pictures, we can do a statistical test. Jarque-Bera tests normality by looking at the skewness and kurtosis. The p-value for the test on the garch residuals is bigger than 10 to the minus 2800. Somewhat smaller than the probability of winning a lottery — but people win lotteries all the time.
Discussion
If we were to consider the hypothetical possibility that returns are not normally distributed, how might that happen?
One way would be if returns across periods did depend on each other. Perhaps if enough people did momentum trades in which they buy because the price has gone up, and sell because the price has gone down.
But of course markets don’t work like that. People trade based on real information (and they evaluate that information without regard to how others value it). News arrives and the market quickly adjusts to that new information.
If data seems to contradict logic, the only civilized thing to do is to stick to logic.
Epilogue
and if you think that you can tell a bigger tale
I swear to God you’d have to tell a lie…
from “Swordfishtrombone” by Tom Waits
Appendix R
qqplot
A simple version of Figure 3 is:
qqnorm(spxret)
qqline(spxret, col="gold")
garch estimate
The GARCH(1,1) model was estimated via:
require(tseries)
spxgar <- garch(spxret)
The QQplot for the residuals was created with:
qqnorm(spxgar$resid[-1])
The square brackets with negative 1 inside them removes the first element of the residual vector (because it is a missing value).
normality test
The tseries package also has the jarque.bera.test function.
> jarque.bera.test(spxgar$resid[-1])
Jarque Bera Test
data: spxgar$resid[-1]
X-squared = 12721.34, df = 2, p-value < 2.2e-16
We get the real p-value (as opposed to the wimpy cop-out of being less than 2.2e-16) with a slight bit of computing:
> pchisq(12721.34, df=2, lower.tail=FALSE, log.p=TRUE) / log(10)
[1] -2762.404
I can hear Nassim Taleb foaming at the mouth…
“But of course markets don’t work like that. People trade based on real information (and they evaluate that information without regard to how others value it). News arrives and the market quickly adjusts to that new information.” It seems as though you livelihood has never depended upon management or performance fees. Talk to portfolio managers and ask them if they ever made a trade of allocation that was contrary to “real information” but instead was based on avoiding making too big of a mistake (career convexity). You may believe that you have the science of investing mastered, but humans – their motivations and incentives – are much too nuanced to fit your rigid ideas. Note that you use 6 decades of data; but, also note that no portfolio managers use 6 decades of data – they use current data and are affected to a great deal by the latest, best conventional wisdom and often get things wrong. Your insistence on normal distributions does not align with the disaster of Long Term Capital Management. They failed because they modeled risk on a normal distribution and woefully underestimated exposure when precision was required to properly manage their leverage.
Pat, I am sorry to say that, but this post is very shallow. I would recommend you to read Nassim Taleb for deeper thoughts. After all, there’s a reason why he is popular nowadays.
Hi,
there is very good work on the distribution of returns by Chris Rogers and Liang Zhang (“Understanding asset returns”)http://www.statslab.cam.ac.uk/~chris/papers/UAR.pdf
I am developing some R code on that but I am not satisfied with the calibration yet.
Best regards,
Richard
Richard,
Thanks for the link, and good luck with the R code. I can believe that it’s a bit tricky to get it to behave.
It is not clear that returns at different time scales should have the same distribution. It could merely be the case that at high frequencies, returns are fat-tailed but have finite variance, and then at low frequencies they are approximately normal. (In fact, barring conditional heteroskedasticity issues, monthly returns do look pretty normal.)
Also, technically speaking, since there is a non-zero probability that a stock’s price may go to zero, there is a non-zero probability that the log return will be (negative) infinity, and thus the variance (and the mean, for that matter) are not well defined. Typically we sweep that possibility under the rug either by survivorship-biasing our sample of stocks or just getting lucky.
Dear Shabby,
Thanks for the comments.
Yes, I think the major problem with the stable distribution idea is that time is infinitely divisible in this context. Once you’re at a time scale on a par with tick data, the distribution is discrete (essentially) with a lot of mass at zero. So it doesn’t look much at all like lower frequency distributions.
I’ll dispute that monthly returns look normal. I just did the Jarque-Bera test on 777 20-day returns of the S&P 500 (the same history as the daily data in the post). It gets a statistic of about 400 which gives a p-value of about 10 the minus 87. So not as extreme as the daily data but still many orders of magnitude smaller than winning a lottery.
I find it intriguing that skewness is much more in evidence at the monthly scale.
Good point about the final value. I think we inherently think about the distribution conditional on survival. That seems reasonably rational to me.
Pingback: A practical introduction to garch modeling | (R news & tutorials) | modelingexcellent.info
This specific blog post, “The distribution of financial
returns made simple | Portfolio Probe | Generate random portfolios.
Fund management software by Burns Statistics” was remarkable.
I’m generating out a duplicate to present to my personal close friends.
Thank you,Galen
Pingback: Popular posts 2012 May | Portfolio Probe | Generate random portfolios. Fund management software by Burns Statistics
Pingback: The US market will absolutely positively definitely go up in 2012 | Portfolio Probe | Generate random portfolios. Fund management software by Burns Statistics
Pingback: A slice of S&P 500 kurtosis history | Portfolio Probe | Generate random portfolios. Fund management software by Burns Statistics
Pingback: A practical introduction to garch modeling | Portfolio Probe | Generate random portfolios. Fund management software by Burns Statistics
Pingback: Popular posts 2012 July | Portfolio Probe | Generate random portfolios. Fund management software by Burns Statistics
Pingback: garch and long tails | Portfolio Probe | Generate random portfolios. Fund management software by Burns Statistics
Pingback: Popular posts 2012 June | Portfolio Probe | Generate random portfolios. Fund management software by Burns Statistics
I am still confusing about returns distribution. please share with me any link for basic understanding of this topic or anyone help me in this topic.
Under the assumption of (relatively) constant market factors, I also suggest that returns are normally distributed. You can find a further neat explanation here: http://www.insight-things.com/distribution-of-stock-return
This is a clear case of showing proof for a thing, and then saying it proves the opposite. I have a hard time believing it is not a troll post.
“One way would be if returns across periods did depend on each other. Perhaps if enough people did momentum trades in which they buy because the price has gone up, and sell because the price has gone down.” Yea, it’s called herding, and, at times of a market crash, it’s called “panic.”
“But of course markets don’t work like that. People trade based on real information (and they evaluate that information without regard to how others value it). News arrives and the market quickly adjusts to that new information.” Everybody values news differently, sometimes jumping to the opposite conclusion. People are rational at that what they do is so that they win, not at being right about their decisions.
“If data seems to contradict logic, the only civilized thing to do is to stick to logic.” Please tell me it’s a joke. I know it’s a joke. Right?
Pingback: Learning things we already know about stocks – Cloud Data Architect
Pingback: Learning things we already know about stocks – Mubashir Qasim
You may find updated information about stock returns distributions in 3-minute video published here:
https://www.indiegogo.com/projects/fat-tails-mathematics/x/17297122#/
if log return has normal distribution, then return has normal distribution too?
No, if log returns have a normal distribution, then simple returns would have a lognormal distribution.
If P2/P1 = ratio of prices at end and beginning of period, then
return = (P2/P1) – 1 = (P2 – P1)/P1
which is usually < 0.10 for daily and monthly periods.
And since log (1 + x) = x for x < 0.10,
So log P2/P1 = log [1 + (P2/P1 – 1)] = P2/P1 -1 = return.
I.e. logs of price ratios = simple returns.
So there is no need to take logs of the price ratios. Using simple returns is sufficient and amounts to the same thing.
Simple returns having a normal distribution is the same thing as return ratios having a lognormal distribution.
And this creates the same technical theoretical problem of a simple return of -100+% having a non-zero probability. This ahould not be a problem because it is only a model valid only within certain limits. Any results involving returns of -100+% are simply nil.