How much does garch shorten long tails?
Previously
Pertinent blog posts include:
- “A practical introduction to garch modeling”
- “The distribution of financial returns made simple”
- “Predictability of kurtosis and skewness in S&P constituents”
Induced tails
Part of the reason that the distributions of returns have long tails is because of volatility clustering. It’s not really the clustering but that volatility changes over time. The returns when volatility is very high will tend to be far in the tails.
One model of volatility clustering is garch. We expect that the standardized residuals from garch models should have shorter tails. That is, be closer to normally distributed.
We look at that with kurtosis. The normal distribution has a kurtosis of 3. Long-tailed means kurtosis is bigger than 3.
Estimation
We model daily log returns of most of the constituents of the S&P 500 over 1547 days. We fit garch(1,1) models assuming either a normal distribution or a Student’s t distribution where the degrees of freedom are estimated.
Figure 1 compares the kurtosis of the standardized residuals between the two garch specifications. You get standardized residuals by subtracting off the mean estimate and then dividing by the estimated standard deviation at each time point. So each standardized residual theoretically has mean 0 and variance 1.
Figure 1: Kurtosis of garch(1,1) residuals assuming either a t or normal distribution.  All of the values are above 3. Some extraordinarily far above.
All of the values are above 3. Some extraordinarily far above.
Figures 2 and 3 compare the garch residual kurtosis to the kurtosis of the returns.
Figure 2: Kurtosis of garch(1,1) residuals assuming a normal distribution compared to that of the returns. 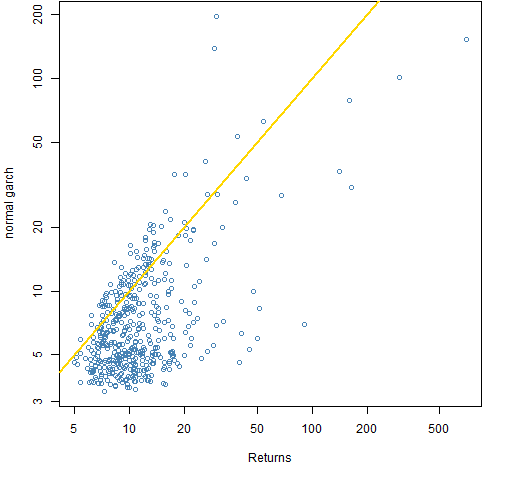
Figure 3: Kurtosis of garch(1,1) residuals assuming a t distribution compared to that of the returns. 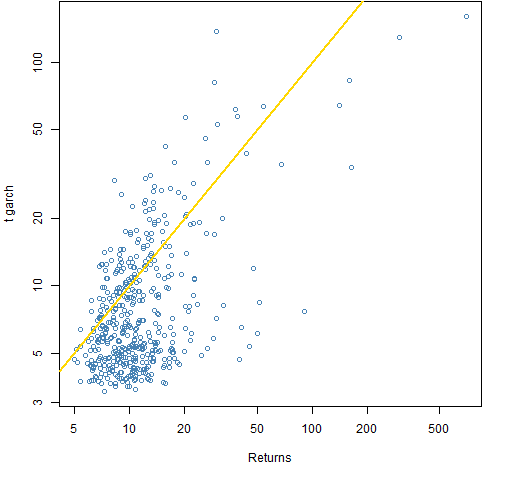 There are two stocks that are outliers in Figure 2 (and less conspicuous in Figure 3) in that they have much lower return kurtosis than garch kurtosis. The explanation turns out to be that there is a robustness issue. Each of them has standardized residuals on the order of 40 (in absolute value) at a big price jump. The two stocks are HAR and THC.
There are two stocks that are outliers in Figure 2 (and less conspicuous in Figure 3) in that they have much lower return kurtosis than garch kurtosis. The explanation turns out to be that there is a robustness issue. Each of them has standardized residuals on the order of 40 (in absolute value) at a big price jump. The two stocks are HAR and THC.
Epilogue
Don’t want no Short People
‘Round here
from “Short People” by Randy Newman
Appendix R
Here is the analysis in R.
estimate garch and get standardized residuals
require(rugarch) tspec <- ugarchspec(mean.model=list(armaOrder=c(0,0)), distribution="std") normspec <- ugarchspec(mean.model=list(armaOrder=c(0,0)), distribution="norm") garnorm.sp <- pp.multFitgarchStanRes(sp5.ret, normspec) gart.sp <- pp.multFitgarchStanRes(sp5.ret, tspec)
clean up
There was one case where the garch estimation didn’t converge, and so there are missing values for that case.
Here we count missing values by column:
> table(colSums(is.na(garnorm.sp))) 0 1547 473 1 > table(colSums(is.na(gart.sp))) 0 474
Now remove that particular stock from both matrices:
garnorm.sp.use <- garnorm.sp[, !is.na(garnorm.sp[1,])] gart.sp.use <- gart.sp[, colnames(garnorm.sp.use)]
estimate kurtosis
require(timeDate) garnorm.kurt <- apply(garnorm.sp.use, 2, kurtosis, method="moment") gart.kurt <- apply(gart.sp.use, 2, kurtosis, method="moment") return.kurt <- apply(sp5.ret[, colnames(garnorm.sp.use)], 2, kurtosis, method="moment")
functions
The functions written for this are in garchkurt_funs.R.

Hi Pat,
cool post!
I was wondering, seems like the std-garch is not enough niether for modelling good tail behaviour. Might be a tough question, but do you have a model in mind that can make figs 2 and 3 more appealing? I think normal and t models do not care much about the empirical kurtosis, maybe something along the lines of ged distribution?
thanks
Eran,
Thanks.
I think that the model dynamics is probably more important than the assumed distribution. I’m guessing that a components model would probably pull the kurtosis in better than the garch(1,1).
In my former life when I was messing with this stuff a lot, I found the t to be better than GED with the components model (and the (1,1)).
I would agree… As long as it is unimodal, symmetric, and has finite variance it really doesn’t matter. Using robust standard deviations, inference should remain reasonably valid???
Pat, what would be interesting is to see how much asymmetric GARCH models reduce skewness.