Exploring the quality of predictions using random portfolios and optimization.
Previously
“Simple tests of predicted returns” showed a few ways to look at expected returns at the asset level. Here we move to the portfolio level.
The previous post focused on correlation. Win Vector Blog points out that gauging prediction quality using correlation can be misleading (because correlation picks the best center for each variable but the center will be fixed in prediction).
Data and model
The universe is 443 large cap US stocks that have data back to the beginning of 2004. The daily (adjusted) close was used.
The model that is used as an example is the default signal from the MACD function of the TTR package in R. This works sometimes, and sometimes not. The signal would need to be scaled to really be expected returns, but the scaling won’t matter for our tests.
Portfolios
Random portfolios with two sets of constraints were generated. They were created as of the information available on 2005 December 15 — one of the dates used in the previous post where the signal worked.
All of the portfolios have the following constraints:
- No asset with weight greater than 10%
- At most 20 assets in the portfolio
- The gross value close to 1 million dollars
One set of portfolios has the additional constraint:
- Long-only
The other set has the constraint:
- Net value between $90,000 and $100,000
That is, a long-short portfolio with a long bias. For long-short portfolios weight is defined as the absolute position size divided by the gross value.
Each set consisted of 1000 portfolios. So — as we’ll see — 6000 portfolios were generated in total.
Correlation with future returns
Figure 1 shows the portfolio “predicted return” versus the subsequent 20-day return for the long-only portfolios. (The “predicted return” is in quotes because of the lack of scaling of the MACD.) Figure 2 is the same for the long-short portfolios.
Figure 1: Portfolio unscaled ex-ante predicted return versus subsequent 20-day return for long-only portfolios. 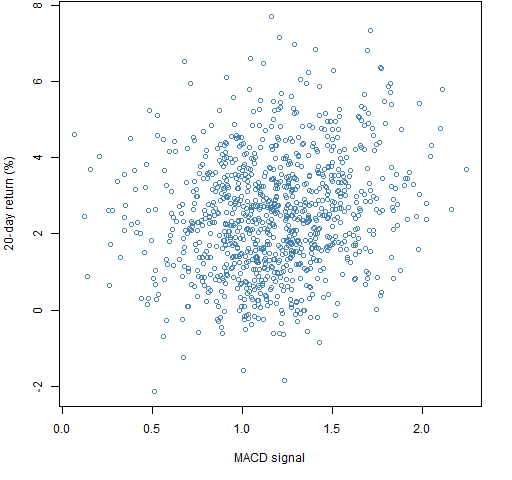
Figure 2: Portfolio unscaled ex-ante predicted return versus subsequent 20-day return for long-short portfolios. 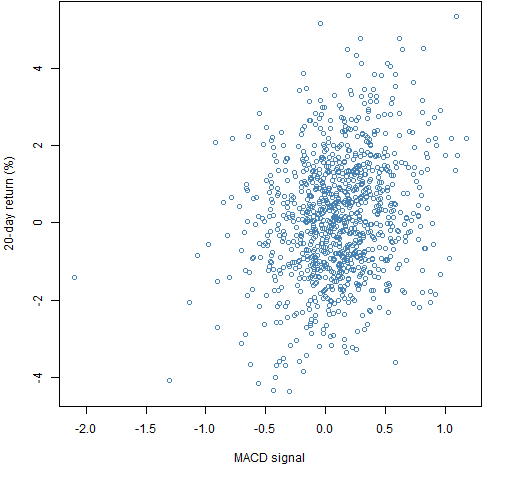 The correlation in Figure 1 (long-only) is about 18% while the correlation for the long-short portfolios is about 23%. The two clouds are in different places. The constraints that are imposed have an impact.
The correlation in Figure 1 (long-only) is about 18% while the correlation for the long-short portfolios is about 23%. The two clouds are in different places. The constraints that are imposed have an impact.
We’re not really interested in typical portfolios though — we’re much more interested in portfolios with extreme values of the expected return. When we optimize the portfolios with these constraints, we get an MACD signal slightly over 5.7 in the long-only case and slightly over 5.5 for long-short. So a long way from the typical values.
Two more sets of portfolios were generated where there was an additional constraint that the expected return needed to be greater than 5. Figures 3 and 4 show results.
Figure 3: Portfolio unscaled ex-ante predicted return of at least 5 versus subsequent 20-day return for long-only portfolios. 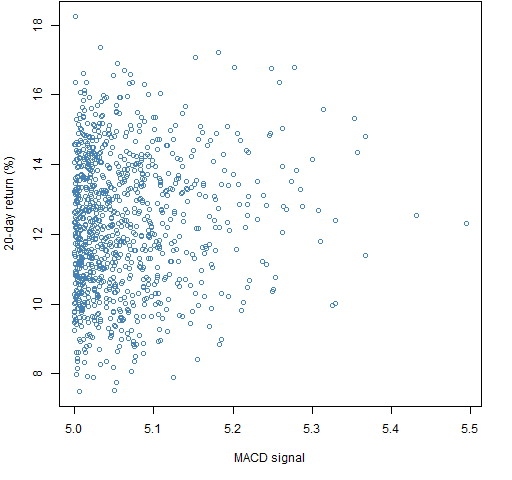
Figure 4: Portfolio unscaled ex-ante predicted return of at least 5 versus subsequent 20-day return for long-short portfolios. 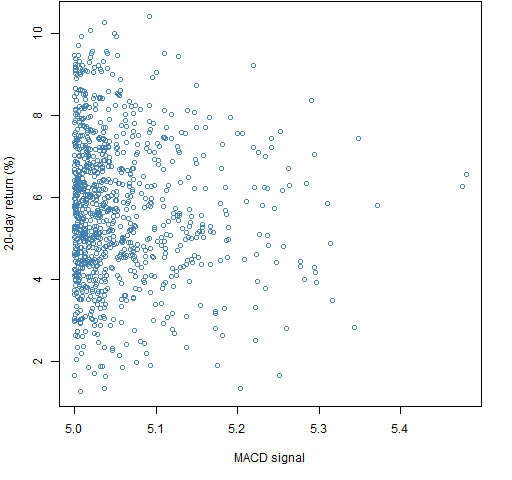 The third pair of sets of random portfolios put the constraints even tighter to the optimal value as shown in Figures 5 and 6.
The third pair of sets of random portfolios put the constraints even tighter to the optimal value as shown in Figures 5 and 6.
Figure 5: Portfolio unscaled ex-ante predicted return of at least 5.7 versus subsequent 20-day return for long-only portfolios. 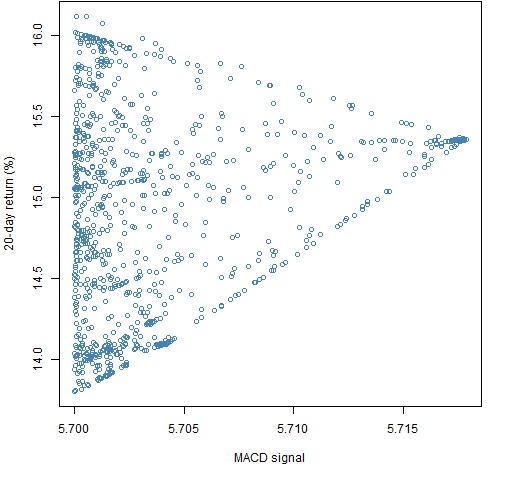
Figure 6: Portfolio unscaled ex-ante predicted return of at least 5.5 versus subsequent 20-day return for long-short portfolios. 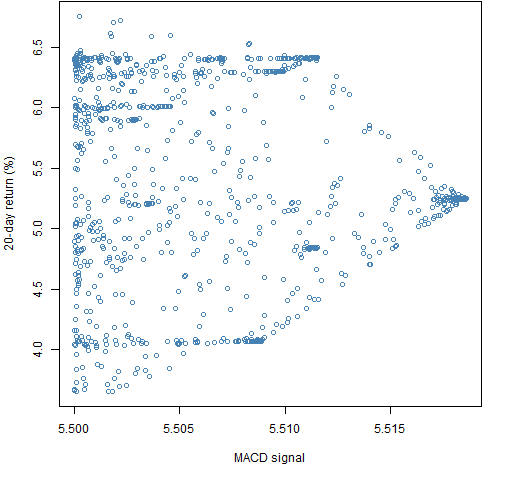 In Figures 5 and 6 we can see the returns narrowing as they home in on the optimal value.
In Figures 5 and 6 we can see the returns narrowing as they home in on the optimal value.
Figure 7 shows boxplots of the returns from the three sets of long-only portfolios. Figure 8 is the same thing for the long-short portfolios.
Figure 7: Realized returns for the three sets of long-only portfolios. 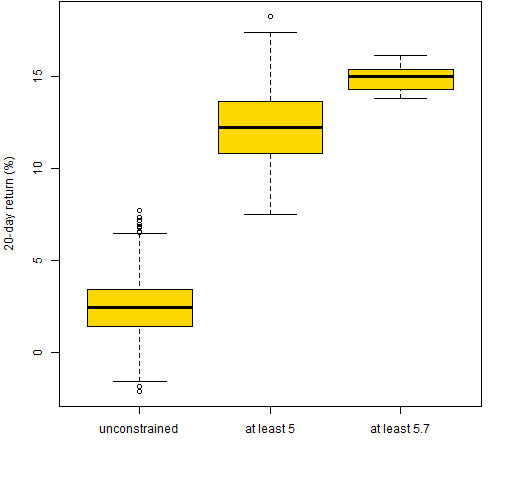
Figure 8: Realized returns for the three sets of long-short portfolios. 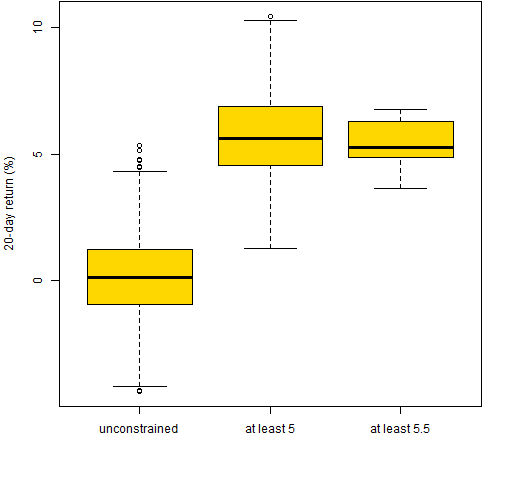 Figure 7 is the textbook version of reality — the closer to optimal, the better. Figure 8 shows the power of the signal maxing out relatively far from the optimal. The closer to the optimum we are restricted, the more luck will be involved in the result.
Figure 7 is the textbook version of reality — the closer to optimal, the better. Figure 8 shows the power of the signal maxing out relatively far from the optimal. The closer to the optimum we are restricted, the more luck will be involved in the result.
Summary
Perfect optimization of trades is not necessary for good results, but it’s hard to know how good is good enough.
Constraints matter.
Epilogue
Throw back the little ones
And pan-fry the big ones
Use tact, poise and reason
And gently squeeze them
from “Throw Back the Little Ones” by Donald Fagen and Walter Becker
Or as Rob (thanks for the suggestion) says, “Steely Dan on portfolio optimization.”
Appendix R
A custom random portfolio function
A function to get the results we want is:
pp.signalrandport <- function(index, times=20,
number.rand=1000, pricemat=tail(univclose130216,
-33), signal=univmacd130216, retmat=univret130216,
...)
{
# placed in the public domain 2013 by Burns Statistics
# testing status: seems to work
require(PortfolioProbe)
signal <- as.matrix(signal)
pricemat <- as.matrix(pricemat)
retmat <- as.matrix(retmat)
if(is.character(index)) {
index <- which(index == rownames(signal))
}
stopifnot(all(rownames(pricemat) == rownames(signal)),
all(rownames(retmat) == rownames(signal)))
rp <- random.portfolio(number.rand=number.rand,
price=pricemat[index,],
expected.return=signal[index,], ...)
alphas <- unlist(randport.eval(rp,
keep="alpha.values"), use.names=FALSE)
futureret <- valuation(rp,
price=pricemat[c(index, index+times),],
returns="log")
list(alphas=alphas, returns=futureret,
randomPortfolios=rp,
date=rownames(signal)[index], call=match.call())
}
This makes sure that the Portfolio Probe software is loaded, generates random portfolios and then finds the expected returns and the realized returns for those portfolios. It depends heavily on the three-dots construct.
Log returns are used because the previous post used them. For this exercise it won’t matter much whether log or simple returns are used.
Generate data
The function from above was used like:
rp51215ls20 <- pp.signalrandport('2005-12-15',
gross.value=1e6, net.value=c(9e4, 1e5),
port.size=20, max.weight=.1)
rp51215lo20 <- pp.signalrandport('2005-12-15',
gross.value=1e6, long.only=TRUE, port.size=20,
max.weight=.1)
The addition of the constraint on the expected value is done like:
rp51215ls20a5 <- pp.signalrandport('2005-12-15',
gross.value=1e6, net.value=c(9e4, 1e5),
port.size=20, max.weight=.1, alpha.constraint=5)
Optimization
The function above was copied and revised to do optimization:
pp.signalopt <- function(index, times=20,
number.rand="not used",
pricemat=tail(univclose130216, -33),
signal=univmacd130216, retmat=univret130216, ...)
{
# placed in the public domain 2013 by Burns Statistics
# testing status: seems to work
require(PortfolioProbe)
signal <- as.matrix(signal)
pricemat <- as.matrix(pricemat)
retmat <- as.matrix(retmat)
if(is.character(index)) {
index <- which(index == rownames(signal))
}
stopifnot(all(rownames(pricemat) == rownames(signal)),
all(rownames(retmat) == rownames(signal)))
trade.optimizer(price=pricemat[index,],
expected.return=signal[index,], ...)
}
It was then used like:
op51215ls20 <- pp.signalopt('2005-12-15',
gross.value=1e6, net.value=c(9e4, 1e5),
port.size=20, max.weight=.1)
Plots
The command to produce Figure 1 is:
plot(rp51215lo20$alpha, rp51215lo20$return * 100, col="steelblue", xlab="MACD signal", ylab="20-day return (%)")
The command to create Figure 7 is:
boxplot(list("unconstrained"=rp51215lo20$return * 100,
"at least 5"=rp51215lo20a5$return * 100,
"at least 5.7"=rp51215lo20a57$return * 100),
col="gold", ylab="20-day return (%)")

Pingback: Predicted correlations and portfolio optimization | Portfolio Probe | Generate random portfolios. Fund management software by Burns Statistics
Pingback: The efficacy of higher moments in portfolio optimization | Portfolio Probe | Generate random portfolios. Fund management software by Burns Statistics