Isn’t the horse facing the cart?
“A New Look At Minimum Variance Investing” by Bernd Scherer (SSRN version) looks at a few aspects of minimum variance portfolios. We’ve been in this neighborhood before with The volatility puzzle solved? This post contains some comments on Bernd’s paper.
Efficient frontiers
My first concern with the paper is footnote 8. This suggests the traditional view via CAPM that you can get a better portfolio with the same risk as the minimum variance portfolio by combining the market portfolio and some amount of the risk-free asset.
First off, do we still believe that a risk-free asset exists?
Figure 1: Efficient frontier for omniscients.
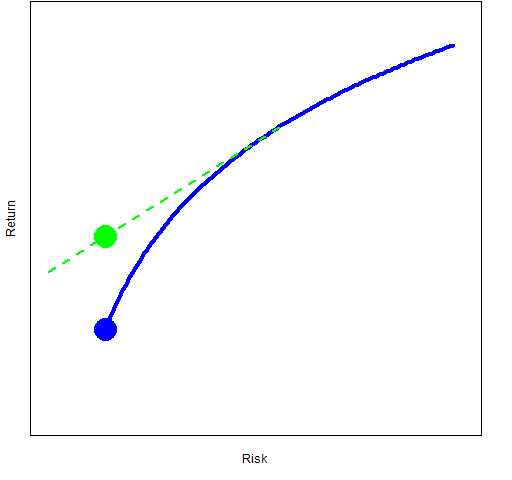
The footnote is suggesting that we select the portfolio represented by the green dot in Figure 1 rather than the minimum variance portfolio (the blue dot). There really is an efficient frontier that looks like this. The problem is that we don’t know how to get it.
Figure 2: Efficient frontier for mortals.

Figure 2 shows the efficient frontier that we really can see. If you ask 100 fund managers to give you the minimum variance portfolio of some universe with specific constraints, then you’ll get 100 portfolios that have some reasonable amount of overlap. More to the point they will behave somewhat similarly. (See What the hell is a variance matrix for an introduction to the predictability of the variance.)
Ask 100 fund managers to give you some other point on the efficient frontier and you’ll get 100 portfolios that look and behave nothing alike.
Performance and anomalies
The paper performs regressions with the minimum variance portfolio relative to the cap-weighted portfolio as the response. The explanatory variables are Fama-French factors, a variable of low beta versus high beta, and a variable of small residual risk versus large residual risk.
The regressions are statistically significant. The paper says that these anomalies explain the good performance of the minimum variance portfolio.
I think that this might be hitching the horse so that it faces the cart. What if those anomalies — that we’ve heard so much about for years — exist because people haven’t been investing in minimum variance portfolios?
Why wouldn’t they? Well, because they’ve been convinced that we know the efficient frontier of Figure 1 and that the tangent portfolio is the market capitalization portfolio. (Table 1 of the paper suggests that the cap-weighted portfolio is unlikely to be anywhere on the efficient frontier.)
Science
Science is the process of creating hypotheses and then trying to undermine or bolster their credibility. Here we have two hypotheses.
Hypothesis 1: The minimum variance portfolio performs well because it happens to overweight known market anomalies.
Hypothesis 2: The known anomalies exist because volatility is systematically ignored in investment decisions.
I see four possibilities:
- Hypothesis 1 is completely correct.
- Hypothesis 2 is completely correct.
- The truth is some combination of Hypotheses 1 and 2.
- There is a third mechanism that is a better explanation than any of the above.
The real science bit is figuring out how to decide among these possibilities.
Section 6 of the paper shows a combination of the cap-weighted portfolio and the beta and residual risk factors outperforming the minimum variance portfolio. This might be thought prima facie evidence against possibility 2. But the results can be explained as merely being at a different spot on or near the efficient frontier.
Kurtosis
Table 1 of the paper shows that the minimum variance portfolio has high kurtosis. Unappetizing as that is, it makes sense. We are tightening down on the volatility as much as we can, but when things go really bad (or really good), the portfolio is going to move. Everyday moves are smaller, extraordinary moves are almost as big — equals higher kurtosis.
Questions
Which way is the horse facing?

[This comment is from Bernd Scherer. It used to be here under his name, but a hardware crash ridded us of that.]
Pat, very nice post.
In my view there is much more estimation error in estimating the minimum variance portfolio than getting efficient portfolios (combinations of cash and market portfolios). The reason is that both minvar and market portfolio suffer from universe selection bias, the minvar also suffers from estimation error and has NO theoretical foundation whatsoever! To reduce risk, I would always take cash!
Nominal riskless asset: long DAX30 short DAX30 future. Gives you a bit less than cash, but should be solid for any practical purpose. Alternatively take short term german bunds. Just dont take OATS.
On the rest I dont think we disagree. I dont really care about the sign of anomaly alphas. My conjecture is that portfolio construction is equal to a mechanical trading strategy that takes implicit bets.
Very much like your kurtosis point!
Great Blog!
Helpful blog, bookmarked the website with hopes to read more!
Pingback: Realized efficient frontiers | Portfolio Probe | Generate random portfolios. Fund management software by Burns Statistics