Casting doubt on the possibility of mean reversion in the S&P 500 lately.
Previously
A look at volatility estimates in “The mystery of volatility estimates from daily versus monthly returns” led to considering the possibility of autocorrelation in the returns. I estimated an AR(1) model through time and added a naive confidence interval to the plot.
With that confidence interval there is a suggestion that there may be mean reversion lately. Gappy, in a comment to that post, is not so sure. He contributed an analysis using a more rigorous method of getting the interval, and used the Bonferroni method to account for multiple comparison.
The plot
Figure 1 shows a slightly prettified version of Gappy’s plot.
Figure 1: Autoregression coefficient of S&P 500 returns with 95% Bonferroni confidence interval. 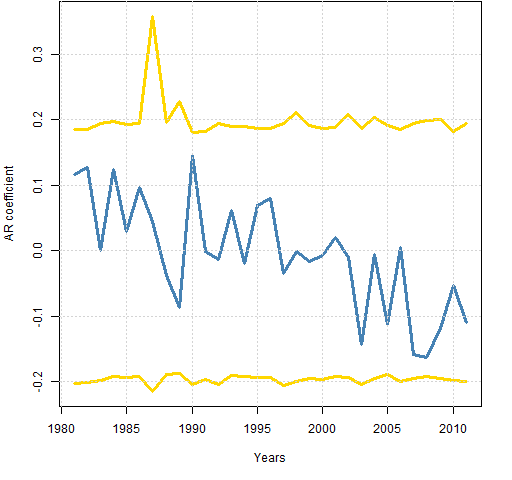 The “years” are not actual calendar years — they end in early November.
The “years” are not actual calendar years — they end in early November.
Comments
Bonferroni limits are conservative (that is, wide). I have no idea how conservative in this case.
I think one of the key things to take away from this plot is the consistency of the interval over time. Changes in volatility don’t seem to affect it.
Given that consistency, my naive confidence interval doesn’t seem so bad after all. The number of years in this plot less than my lower limit looks to be at least 3 (out of 31), or almost 10%. Since that is more than 5%, that would argue towards mean reversion.
But if we don’t want to believe that there was positive autocorrelation in this period, then noting that the tails of the current estimates are reasonably symmetric around zero would argue against mean reversion.
Another point in favor of mean reversion is the downward trend of the AR coefficient. However, we can easily be fooled into thinking there is a trend when there is not one.
Appendix R
The analysis was done with:
source('spxanalysis.R')
Actually that was step 3. Step 1 was saving the file to my computer (optional). Step 2 was starting R.
This highlights some of the power of R. In less than 40 lines Gappy created quite a sophisticated analysis and then could transmit that so that anyone* can reproduce it with one trivial command.
* “anyone” is hyperbole — you need a computer with internet access.

It occurs to me that some people might like some further elucidation on the difference between the two types of confidence interval — the one in Figure 1 here versus the one in Figure 5 of the previous post.
They are both 95% confidence intervals, but they are very different numerically even though they use essentially the same technology. The difference is in the interpretation.
The confidence interval in Figure 1 in this post is saying that if there were no autocorrelation, then if we did this process numerous times on different data, then we would expect at least one estimate to fall outside the interval for about 5% of the datasets. Almost all datasets have no points outside the interval.
The confidence interval in Figure 5 of the previous post is saying that if there were no autocorrelation, then we expect about 5% of the points in the plot to fall outside the interval. (So for any one dataset we expect some points outside the interval.)
Actually, that isn’t quite right because the points in the plot in Figure 5 are use overlapping data. The statement is correct if we look at only the points with non-overlapping data — one point per year.
Hi
Thanks for the post.
Why not construct a more “standard” CI?
AR(1) coefficients amounts to a standard “RHO” between the window(t) and window (t-1) vectors. It is approximately normal at every time point. I am not sure bootsrap is the way to go, and Bonferroni method is more for independent tests, while (I think) this is a rolling window.
Thanks
Thanks for your comments.
One reason to use the bootstrap is that we don’t need to worry about the distribution of the data and hence of the statistic. Another reason is Uwe’s Maxim: computers are cheap and thinking hurts.
I used rolling windows, but when Gappy did the Bonferroni limits it was on non-overlapping data.
Going back to Pat’s original post commenting on dailly vs. annualised returns, can anyone help with the following?
I am currently examining return & volatility data for various portfolio asset mixes to ascertain optimum risk adjusted returns.
The dataset I have goes back to 1988.
If I use annual returns there are fewer data points for comparison but if I use monthly data annualised this suffers from not being precisely accurate.
Any comments are hugely appreciated.
Pingback: The volatility mystery continues | Portfolio Probe | Generate random portfolios. Fund management software by Burns Statistics