Some thoughts and resources regarding a popular fund management buzzword.
The idea
Given asset categories (like stocks, bonds and commodities) create a portfolio where each category contributes equally to the portfolio variance.
Two operations
There are two cases in creating a risk parity portfolio:
- the universe is the asset categories
- the universe is the assets within the categories
In the first case the resulting portfolio is completely defined by the assumed variance matrix. If we demanded an equal weight portfolio, then how much we had of each asset would be completely determined by the prices of the assets. The same thing happens with risk parity.
In the second case there is more freedom. The portfolio variance can vary along with the specific assets that are included and their weights.
Assumptions
What do we need to believe in order to want a risk parity portfolio?
We might naively think that it has to do with the equality of the utility of the categories. As we’ll see that is sometimes true, but it depends on our utility.
We’ll use the stock-bond data given in Asness, Frazzini and Pedersen (Table 2, page 22). This lists the excess return of stocks as 5.96% with volatility of 15.71%, and the excess return of bonds 2.72% with 5.36% volatility. We also assume the case that the universe is just the two categories: stocks and bonds.
mean-variance utility
With this data and assuming that we have a mean-variance utility (portfolio return minus portfolio variance times risk aversion — no 2 involved), we look at what the correlation between stocks and bonds must be in order to get the risk parity portfolio. Figure 1 shows the results.
Figure 1: Required stock-bond correlation to get risk parity portfolio with mean-variance utility. 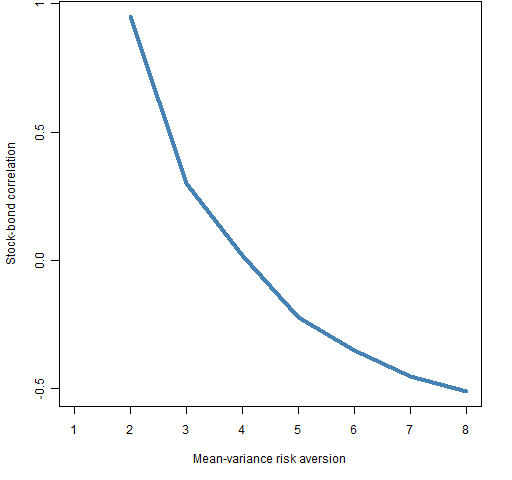
You can see that if you have a risk aversion of 1 that you can’t get the risk parity portfolio. The required correlation is highly dependent on risk aversion.
maximum information ratio utility
If the task is to maximize the information ratio (actually the Sharpe ratio since excess returns are used), then we need to increase the excess return of stocks to 7.97% in order to get the risk parity portfolio — this makes the information ratio of stocks equal to that of bonds. The correlation between the categories doesn’t matter.
Thought experiment
Suppose we have a risk parity portfolio of stocks and bonds and then we want to add commodities. The risk of commodities suddenly goes from zero to one-third. If we then split bonds into government bonds and corporate bonds, then the total amount of risk in bonds goes from one-third to one-half.
Is this rational?
In Portfolio Probe
universe is categories
This would just take an additional argument in the optimizer:
risk.fraction = 1/Nassets + eps
The eps is needed because of the discreteness of trading. It would be sufficient to make eps the largest unit cost divided by the gross value of the portfolio.
universe is assets within categories
The constraint bounds would be set like:
linB[categRows, 2] <- 1/Ncateg + eps
and then optimizer arguments (available as of version 1.04) would be:
lin.bounds=linB, lin.style="varfraction"
Resources
A lot of documents on risk parity are written either to promote it, or to tear it apart.
Pro
“Leverage Aversion and Risk Parity” by Clifford Asness, Andrea Frazzini and Lasse Pedersen.
“Risk parity: Case study: ATP” by Henrik Gade Jepsen.
“Counter-Point to Risk Parity Critiques” by Ed Peters.
Con
“Risk Parity: Nice idea, awkward reality” by Joseph Mariathasan.
“The Hidden Risks of Risk Parity Portfolios” by Ben Inker.
“The Perils of Parity” by Ruban and Melas. Mostly about leverage. Free registration is required.
General
“Risk Parity 101” from Hammond Associates.
Special issue of The Journal of Investing on risk parity from Spring 2011.
“Risk Parity: In the spotlight after 50 years” by Christopher Levell.
“Survey Finds Asset Owners ‘Get’ Risk Parity” from Plan Sponsor.
“On the Properties of Equally-Weighted Risk Contributions Portfolios” by Maillard, Roncalli and Teiletche.
“Risk Parity Portfolio vs. Other Asset Allocation Heuristic Portfolios” by Chaves, Hsu, Li and Shakernia.
Update
Resources added after the initial posting:
World Beta has a post that includes risk parity references and a bit of history.
“Risk Parity — Rewards, Risks and Research Opportunities” by Barry Schachter and S. Ramu Thiagarajan
“Risk Parity for the Masses” by Andreas Steiner
A list of risk parity references from Investment and Pensions Europe
“Will My Risk Parity Strategy Outperform?” by Robert Anderson, Stephen Bianchi and Lisa Goldberg.
“Risk Parity Research Summary, May 2012” from Empiritrage.
My take
A good thing about risk parity is that it emphasizes constraints on risk rather than weights. Now that we have technology to impose constraints on partitions of the portfolio variance it would be good for weight constraints to largely go extinct.
Some of the good features of risk parity is because it moves toward low volatility investing.
The bad part of risk parity is that — in my opinion — it over-constrains portfolios. Neither am I especially keen on leveraging to make the overly constrained portfolio have an expected return similar to a less constrained portfolio.
Questions
What am I missing or have wrong regarding what risk parity means?
What am I missing in the way of resources?
Appendix R
Some R functions that were used to create the analyses are in risk_parity_objs.R.
For instance finding the stock return for the risk parity with different correlations when maximizing the information ratio was done with:
require(PortfolioProbe)
rhovec2 <- seq(-.1, .3, length=50)
irstockret <- numeric(50)
names(irstockret) <- rhovec2
for(i in 1:50) irstockret[i] <- uniroot(function(x) pp.sbir(rhovec2[i], x), c(0,.5))$root

You are right that risk parity portfolios are very sensitive to the choice of the investment universe, and slicing it differently or adding new assets classes can be disruptive. Allocation can become tricky with highly substituable assets in the mix.
Leveraging the portfolio is a choice: the basic algorithm just says to divide the risk evenly, without necessarily adjusting the resultant volatility.
The main benefit of the approach is to force people to think in terms of contributions rather than exposure. You can combine it with a traditional approach adding for instance a penalty term when deviating from risk parity to a max Sharpe program.
TM, thanks for your comments.
I agree with your assessment of the main benefit — that it is getting people to think differently. In that sense I think it is very valuable.
Emphasizing that leverage is really a separate issue is useful. However, it looks to me like the selling of funds isn’t always done that way.
There was a slightly ironic twist in the data values that I used for stocks and bonds: the maximum information ratio portfolio (for essentially all correlations) has more weight in bonds than the risk parity portfolio. The 60/40 portfolio is far, far away from maximizing the information ratio.
Much of the media and commentary treat Risk Parity (RP) as if it were only applicable to asset categories, so thank you for pointing out that it can apply to assets within categories. I think RP offers a valid portfolio construction method when the investor doesn’t have explicit return expectations AND the investor doesn’t want to be too concentrated in the largest assets of the category.
“Some of the good features of risk parity is because it moves toward low volatility investing.”
I used to believe that too, but I have discovered it’s actually a tendency, not a truism. Contribution to portfolio risk is a function of volatility AND weight in the portfolio; so it’s more accurate to say it moves toward low volatility AND smaller cap.
Example: Try building a Risk Parity portfolio of stocks within the S&P 500 Energy sector. I did this in the Spring, and here’s what I found: since ExxonMobil (XOM), one of the lowest volatility stocks in the sector is the biggest stock in the sector, XOM got underweighted in the RP allocation due to its size, not due to its volatility. As a result, the Energy RP allocation actually had a somewhat higher volatility than a market weight allocation would since it so underweighted XOM.
Tom,
That seems like quite a reasonable point to me — that you can find an “optimal” portfolio that is completely determined by the risk parity constraint. It is relatively painless and should be reasonably stable.
We do seem to have a difference of opinion on the suitability of spreadsheets however.
I realize that a clarification may be in order. Risk parity is very often presented in the realm of equal contribution from stocks and bonds, or something similar. In this case the fraction of stocks versus bonds is determined by the risk parity constraint.
Tom is wanting to impose the risk parity constraint on a portfolio of individual stocks so that each stock contributes the same amount of variance to the portfolio. This again completely determines the portfolio.
An example of “assets within categories” in the way that I have in mind is that we want the variance contribution from stocks to be equal to the variance contribution from bonds. But we are building the portfolio from a number of stocks and a number of bonds. In this case the portfolio is not completely determined by the risk parity constraint — there will be a lot of choice in the specific assets chosen for the portfolio and their weights.
Pingback: Risk Parity Portfolios Aren’t Always Less Volatile Than Market Weight Portfolios » Investment Solutions - Portfolio Construction Experts | PortfolioWizards
Pingback: Sensitivity of risk parity to variance differences | Portfolio Probe | Generate random portfolios. Fund management software by Burns Statistics
Pingback: How do you remove expected returns from asset allocation strategies? | CL-UAT